Principal component analysis (PCA) is an unsupervised classification method. However, the PCA method in DataPandit cannot be called an unsupervised data analysis technique as the user interface is defined to make it semi-supervised. Therefore, let’s look at how to perform and analyze PCA in DataPandit with the help of the Iris dataset.
Arranging the data
There are some prerequisites for analyzing data in the magicPCA application as follows:
- First, the data should be in .csv format.
- The magicPCA application considers entries in the first row of the data set as column names by default.
- The entries in the data set’s first column are considered row names by default.
- Each row in the data set should have a unique name. I generally use serial numbers from 1 to n, where n equals the total number of samples in the data set. This simple technique helps me avoid the ‘duplicate row names error.’
- Each column in the data set should have a unique name.
- As magicPCA is a semi-supervised approach, you need to have a label for each sample that defines its class.
- There should be more rows than the number of columns in your data.
- It is preferable not to have any special characters in the column names as the special characters can be considered mathematical operations by the magicPCA algorithm.
- The data should not contain variables with a constant value for all the samples.
- The data should not contain too many zeros.
- The data must contain only one categorical variable
Importing the data set
The process of importing the data set is similar to the linear regression example. You can use the drag and drop option or the browse option based on your convenience.
Steps in data analysis of PCA
Step 1: Understanding the data summary
After importing the data, it makes sense to look at the minimum, maximum, mean, median, and the first and third quartile values of the data to get a feel of the distribution pattern for each variable. This information can be seen by going to the ‘Data Summary’ tab beside the ‘Data’ tab in the main menu.
Step 2: Understanding the data structure
You can view the data type for each variable by going to the ‘Data Structure’ tab beside the ‘Data Summary’ tab. Any empty cells in the data will be displayed in the form of NA values in the data structure and data summary. If NA values exist in your data, you may use data pre-treatment methods in the sidebar layout to get rid of them.
Step 3: Data Visualization with boxplot
As soon as the data is imported, the boxplot for the data gets automatically populated. Boxplot can be another valuable tool for understanding the distribution pattern of variables in your data set. You can refer to our earlier published article to learn how to use boxplot.
You can mean center and scale data set to normalize the distribution pattern of the variables.
The following picture shows the Iris data when it is mean-centered.
The picture below shows the Iris data when it is scaled after mean centering.
Step 4: Understanding the multicollinearity
Multicollinearity of the variables is an essential prerequisite for building a good PCA model. To know more about multicollinearity and how to measure it read our article on Pearson’s correlation Coefficient and how to use the multicollinearity matrix.
Step 5: Divide the data in the training set and testing set
After importing the data, the training and testing data set automatically gets selected based on default settings in the application. You can change the proportion of data that goes in the training set and testing set by Increasing or decreasing the value for the ‘Training Set Probability’ in the sidebar layout, as shown in the picture below.
Suppose the value of the training set probability is increased. In that case, a larger proportion of data goes into the training set whereas, if the value is decreased, the relatively smaller proportion of data remains in the training set. For example, if the value is equal to 1, then 100% of the data goes into the training set living testing set empty.
As a general practice, it is recommended to use the training set to build the model and the testing set to evaluate the model.
Step 6: Select the column with a categorical variable
This is the most crucial step for building the PCA model using DataPandit. First, you need to select the column which has a categorical variable in it. As soon as you make a selection for the column which has a categorical variable, the model summary, plots, and other calculations will automatically appear in under the PCA section of the ‘Modal Inputs’ tab in the Navigation Panel.
Step 7: Understanding PCA model Summary
The summary of PCA can be found below the model summary tab.
The quickest way to grasp information from the model summary is to look at the cumulative explained variance, which is shown under ‘Cumexpvar,’ and the corresponding number of components shown as Comp 1, Comp 2, Comp 3, and so on. The cumulative explained variance describes the percentage of data represented by each component. In the case of the Iris data set, the first component describes 71.89% of the data (See Expvar). At the same time, the second component represents 24.33% of the data. Together component one and component two describe 96.2 2% of the data. This means that we can replace the four variables which describe one sample in the Iris data set with these two components that describe more than 95% of the information representing that sample in the data set. And this is the precise reason why we call principal component analysis as a dimensionality reduction technique.
Step 8: Understanding PCA summary plot
The PCA summary plot shows scores plot on the top left side, loadings plot on the top right side, distance plot on the bottom left side, and cumulative variance plot on the bottom right side. The purpose of the PCA summary plot is to give a quick glance at the possibility of building a successful model. The close association between calibration and test samples in all the plots indicates the possibility of creating a good model. The scores plot shows the distribution of data points with respect to the first two components of the model.
In the following PCA summary plot, the Scores plot shows two distinct data groups. We can use the loadings plot to understand the reason behind this grouping pattern. We can see in the loading plot that ‘sepal width’ is located father from the remaining variables. Also, it is the only variable located at the right end of the loadings plot. Therefore we can say that the group of samples located on the right side of the scores plot is associated with the sepal width variable. These samples have higher sepal width as compared to other samples. To reconfirm this relationship, we can navigate to the individual scores plot and loadings plot.
Step 9: Analyzing Scores Plot in PCA
The model summary plot only gives an overview of the model. It is essential to take a look at the individual scores plot to understand the grouping patterns in more detail. For example, in the model summary plot, we could only see two groups within the data. However, in the individual scores plot we can see three different groups within the data: setosa, versicolor, and virginica. The three groups can be identified with three different colors indicated by the legends at the top of the plot.
Step 10: Analyzing loadings plot in PCA
It is also possible to view individual loadings plot. To view it, select ‘Loadings Plot’ option under the ‘Select the Type of Plot’ in the sidebar layout.
The loadings plot will appear as shown in the picture below. If we compare the individual scores plot and loading plot, we can see that the setosa species samples are far away from the verginica and the Versicolor species. The location of the Setosa species is close to the location of sepal width on the loadings plot, which means that the setosa species has higher sepal with as compared to the other two species.
Step 11: Analyzing distance plot in PCA
You can view the distance plot by selecting the ‘Distance Plot’ option under the ‘Select the Type of Plot’ in the sidebar layout. The distance plot is used to identify outliers in the data set. If there is an outlier, it will be located far away from the remaining data points on this plot. However, the present data set does not have any outliers. Hence we could not spot any. Ideally, you should never label a sample as an outlier unless and until you know a scientific or practical reason which makes it an outlier.
Step 12: Analyzing explained variance plot in PCA
You can view explained variance plot by selecting the ‘Explained Variance Plot’ option under the ‘Select the Type of Plot’ in the sidebar layout. It shows the contribution of each principal component in describing the data points. For example, in this case, the first principal component represents 71.9 % of the data whereas the second principal component describes 24.3% of the data. This plot is used to find out the number of principal components that can optimally describe the entire data. It is expected that the optimal number of components should be lower than the total number of columns in your existing data set because the very purpose of a PCA model is to reduce the dimensionality of the data. In the case of the Iris data, we can say that two principal components are good enough to describe more than 95% of the data. Also, addition of more principal components does not result in a significant addition to the information (<5%). Pictorially, we can also come down to this conclusion by identifying the elbow point on the plot. The elbow point, in this case, is at principal component number 2.
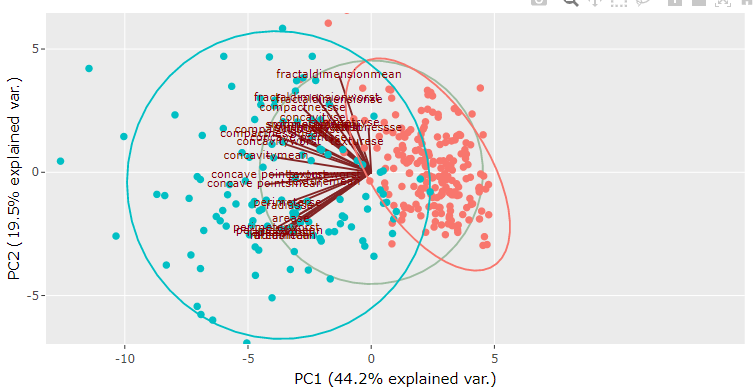
Step 13: Analyzing biplot in PCA
The biplot for PCA shows scores and the loading information on the same plot. For example, in the following plot, we can see that loadings are shown in the form of lines that originate from a common point at the center of the plot. At the same time, scores are shown as scattered points. The direction of the loadings line indicates the root cause for the location of the samples on the plot. In this case, we can see that setosa samples are located in the same direction as that of the sepal width loading line, which means that setosa species have higher sepal width than the other two species. It reconfirms our earlier conclusion drawn based on individual scores and loadings plot.
Step 14: Saving the PCA model
If you are satisfied with the grouping patterns in the PCA model, then you can go on to build an individual PCA model for each categorical level. Therefore, in the case of the Iris data, we need to make 3 PCA models, namely, setosa, virginica, and Versicolor. To do this, we need to navigate to the SIMCA option under the ‘Model Inputs’ option in the navigation panel.
After going to the SIMCA option, select the species for which you want to build the individual model using the drop-down menu under ‘Select One Group for SIMCA Model.’ As soon as you select one group, the SIMCA model summary appears under ‘SIMCA Summary’ in the main menu. Depending on the cumulative explained variance shown under the ‘Simca Summary’, select the number of components for SIMCA using the knob in the sidebar layout. Save individual model files for each categorical level using ‘Save File’ button under the ‘Save Model’ option in the sidebar layout.
Step 16: Uploading PCA Models for SIMCA predictions
You can upload the saved individual model files using the ‘Upload Model’ feature in the sidebar layout.
To upload the model files, browse to the location of the files in your computer, select the ‘All files’ option in the browsing window, Press’ ctrl’, and select all the model files for the individual models as shown in the picture below.
Step 17: Understanding the result for the train set
As soon as the individual model files are uploaded, the predictions for the train set and test set populate automatically. Go to the ‘Train SIMCA’ tab to view the predictions for the train set . You can see the predictions for individual sample by looking at the table which displays on the screen under the ‘Train SIMCA’ tab. In the prediction table, 1 indicates the successful classification of the sample into the corresponding category represented by column name. However, it may not be convenient to check the classification of each sample in the training data. Therefore, to avoid this manual work, you can scroll down to see the confusion matrix.
The confusion matrix for the train set of Iris data is shown in the figure below. The rows of the confusion matrix represent the actual class of the sample, whereas the columns of the confusion Matrix represent the predicted class of the sample. Therefore, the quickest way to analyze the confusion matrix is to look at the diagonal elements and non-diagonal elements of the matrix. Every non-diagonal element in the confusion matrix is misclassified and contributes to the classification error. If there are more non-diagonal elements than the diagonal elements in your confusion Matrix, then that means the models cannot distinguish between different classes in your data. For example, in the case of Iris, data following confusion matrix shows that four Versicolor samples are misclassified as Verginaca, and one sample from each class could not be classified into any species. The model’s accuracy can be calculated by performing a sum of correctly classified samples and dividing it by the total number of samples in the training set. In this case, accuracy will be equal to the sum of diagonal elements divided by the total number of samples in the train set. At the same time, the misclassification error can be found by subtracting the accuracy from 1.
The closer the accuracy value to 1, the better the model’s predictability.
The Confusion Matrix can be pictorially seen by going to the ‘Train SIMCA plot’ option in the main menu. The plot shows the three species in three different colours, represented by the legend at the top.
You can view cooman’s plot by selecting Cooman’s Plot’ or the ‘Model Distance Plot’ option in the ‘Model Plot Inputs’ in the sidebar layout.
Cooman’s plot shows squared orthogonal distance from data points to the first two selected SIMCA (individual PCA) models. The points are color grouped according to their respective class in the case of multiple result objects.
‘Model Distance Plot’ is a generic tool for plotting distance from the first model class to other class models.
Step 18: Understanding the result for the test set
The process of analyzing the results for the test set is the same as that of the train set. The results for the test set can be found under the ‘Test SIMCA’ and the ‘Test SIMCA Plot.’
Step 19: Predict the unknown
If you are happy with the train set and test set results, you can go ahead and navigate to the ‘Predict’ option in the Navigation Panel. Here you need to upload the file with samples from unknown class and the individual models using the process similar to step 16. And the Prediction Plot will populate automatically.
Conclusion
Principal Component Analysis is a powerful tool for material characterization, root cause identification, and differentiating between the groups in the data. In addition, DataPandit’s magicPCA makes it possible to predict of the unknown class of data with the help of a dataset with known classes of samples.
Need multivariate data analysis software? Apply here for free access to our analytics solutions for research and training purposes!