magicPCA

Introduction

Principal Component Analysis (PCA) is a statistical technique used to reduce the dimensionality of a dataset by transforming the data into a new coordinate system. It works by identifying patterns in the correlations between the variables in the original dataset and constructing a new set of variables, called principal components, which capture as much of the variation in the data as possible.
Our SaaS Cloud Platform will provide a web-based solution useful to understand data groupings in highly dimensional data.
Our SaaS Cloud Platform will provide access to PCA and SIMCA algorithm anytime, anywhere.

Why choose magicPCA?

Dimensionality reduction: PCA is commonly used to reduce the dimensionality of high-dimensional data sets. It can transform a large number of variables into a smaller number of principal components, which can capture the most important information in the data. This makes it easier to visualize and analyze the data.
Feature extraction: PCA can be used to extract relevant features from the data. By transforming the data into a new coordinate system, it can identify patterns in the correlations between the variables, and construct a set of new variables that capture the most important information. These new variables, called principal components, can be used as features for machine learning algorithms.
Data visualization: PCA can be used to visualize high-dimensional data in lower-dimensional spaces, such as 2D or 3D plots. This can help to identify patterns and relationships between variables that may not be apparent in the original high-dimensional data.
Noise reduction: PCA can help to reduce noise in the data by eliminating small variations and retaining the most important patterns. This can improve the accuracy of machine learning models.
Multicollinearity reduction: PCA can also help to address multicollinearity, which is a common problem in regression analysis when predictor variables are highly correlated. By reducing the number of variables and transforming them into orthogonal principal components, PCA can help to address multicollinearity and improve the accuracy of regression models.

Applications of magicPCA:

Finance

Portfolio optimization: PCA can be used to identify the key sources of risk and return in a portfolio, and to optimize the portfolio weights accordingly. This can help investors to achieve their desired risk-return tradeoff and to diversify their holdings.
Risk management: PCA can be used to identify the key drivers of risk in a financial market, such as interest rates, exchange rates, and market volatility. This can help investors to manage their exposure to these risks and to hedge against potential losses.
Asset pricing: PCA can be used to identify the underlying factors that drive asset prices, such as macroeconomic variables, industry trends, and company fundamentals. This can help investors to understand the true value of assets and to make more informed investment decisions.
Credit risk analysis: PCA can be used to analyze the creditworthiness of borrowers by identifying the key factors that contribute to default risk, such as income, debt levels, and credit history.
Market forecasting: PCA can be used to analyze historical market data and to identify patterns that can be used to predict future market trends and movements.

Marketing

Market segmentation: PCA can be used to segment customers into groups based on shared characteristics, such as demographic, behavioral, or psychographic factors. This can help marketers to tailor their messaging and products to each segment and to improve overall marketing effectiveness.
Brand positioning: PCA can be used to analyze brand perception and to identify key drivers of brand positioning. This can help marketers to develop brand strategies that align with customer needs and preferences.
Product development: PCA can be used to analyze customer feedback and to identify key product features and attributes that are most important to customers. This can help marketers to develop products that are better aligned with customer needs and preferences.
Customer satisfaction analysis: PCA can be used to analyze customer satisfaction data and to identify key drivers of customer satisfaction. This can help marketers to improve customer experience and to retain loyal customers.
Campaign optimization: PCA can be used to analyze campaign data and to identify key drivers of campaign success, such as messaging, targeting, and creative. This can help marketers to optimize their campaigns for better performance and ROI.

Healthcare

Disease diagnosis: PCA can be used to analyze patient data and to identify key risk factors for a particular disease. This can help clinicians to diagnose diseases earlier and to develop targeted treatment plans.
Treatment optimization: PCA can be used to analyze patient data and to identify key factors that contribute to treatment success or failure. This can help clinicians to develop personalized treatment plans that are better aligned with patient needs and preferences.
Patient stratification: PCA can be used to identify subgroups of patients with similar disease characteristics, treatment responses, or outcomes. This can help clinicians to tailor treatment plans to each patient subgroup, leading to improved treatment effectiveness.
Drug discovery: PCA can be used to analyze large datasets of drug and disease data and to identify key factors that contribute to drug efficacy or toxicity. This can help researchers to develop new drugs that are better targeted and more effective.
Health outcomes analysis: PCA can be used to analyze large datasets of patient health outcomes and to identify key factors that contribute to health disparities or inequalities. This can help policymakers to develop targeted interventions that improve health outcomes for disadvantaged populations.

Attitude and opinion analysis: PCA can be used to analyze survey data and to identify key factors that contribute to attitudes and opinions on a particular topic. This can help researchers to understand the underlying factors that shape public opinion and to develop targeted interventions that change attitudes and behaviors.
Psychometric analysis: PCA can be used to analyze survey data and to identify key factors that contribute to psychological constructs such as personality, motivation, and emotion. This can help researchers to develop more accurate and reliable measures of these constructs, and to better understand the underlying factors that contribute to human behavior.
Education research: PCA can be used to analyze student data and to identify key factors that contribute to academic achievement, such as test scores, attendance, and behavior. This can help educators to develop targeted interventions that improve student outcomes and to identify students who may be at risk of academic failure.
Consumer behavior analysis: PCA can be used to analyze consumer data and to identify key factors that contribute to consumer behavior, such as purchasing decisions and brand loyalty. This can help marketers to develop more effective marketing strategies and to better understand the factors that drive consumer behavior.
Social inequality analysis: PCA can be used to analyze large datasets of social and economic data and to identify key factors that contribute to social inequality, such as income, education, and race. This can help policymakers to develop targeted interventions that reduce social inequalities and promote social justice.

Manufacturing

Quality control: PCA can be used to identify the key factors that influence the quality of a product. By analyzing the variance of the data, PCA can help manufacturers identify the variables that have the greatest impact on product quality, and prioritize efforts to improve those variables.
Process optimization: PCA can help manufacturers identify the key variables that affect the performance of a manufacturing process. By analyzing the correlation between the variables, PCA can help manufacturers optimize the process by adjusting the variables that have the greatest impact on the output.
Fault detection and diagnosis: PCA can be used to detect anomalies in the manufacturing process by analyzing the variance of the data. By monitoring the principal components, manufacturers can identify when the process is deviating from normal operation and take corrective action before it affects the quality of the product.
Product design: PCA can be used to identify the key features that differentiate a product from its competitors. By analyzing the variance of the data, PCA can help manufacturers identify the design elements that have the greatest impact on customer preferences, and prioritize efforts to improve those elements.
Supply chain optimization: PCA can be used to analyze the performance of suppliers and identify the key factors that affect their performance. By analyzing the correlation between the variables, manufacturers can optimize their supply chain by prioritizing suppliers that have the greatest impact on their output.

Business intelligence

Data reduction: PCA can be used to reduce the dimensionality of large datasets, which can be useful in data analysis and visualization. By reducing the number of variables, PCA can simplify the data and make it easier to understand and interpret.
Feature extraction: PCA can help identify the most important features or variables in a dataset. This can be useful in various applications such as recommendation systems, fraud detection, and predictive modeling.
Anomaly detection: PCA can be used to detect anomalies or outliers in data. By analyzing the variance of the data, PCA can identify patterns that deviate from the norm, which can be indicative of fraudulent activity, errors, or other unusual events.
Clustering: PCA can be used to group similar data points together. By analyzing the correlation between variables, PCA can help identify clusters of data points that have similar characteristics, which can be useful in segmentation analysis and customer profiling.
Visualization: PCA can be used to visualize high-dimensional data in a lower-dimensional space. By projecting data onto a two-dimensional plane, for example, PCA can help visualize the relationships between variables and identify patterns that may not be visible in higher dimensions.

Chemical Sector

Quality control: PCA can be used to identify the key factors that influence the quality of chemical products. By analyzing the variance of the data, PCA can help identify the variables that have the greatest impact on product quality, and prioritize efforts to improve those variables.
Process optimization: PCA can help optimize chemical processes by identifying the key variables that affect the performance of the process. By analyzing the correlation between the variables, PCA can help adjust the variables that have the greatest impact on the output, leading to improved process efficiency and reduced costs.
Product development: PCA can be used in chemical product development to identify the key components that influence the properties of the product. By analyzing the variance of the data, PCA can help identify the components that have the greatest impact on the product’s properties, and optimize the product composition to improve its performance.
Risk assessment: PCA can be used in the chemical industry to assess risks associated with the handling and processing of chemicals. By analyzing the correlation between variables, PCA can help identify potential risks and develop strategies to mitigate them.
Environmental monitoring: PCA can be used to analyze environmental data in the chemical industry. By analyzing the variance of the data, PCA can help identify the sources of pollutants and prioritize efforts to reduce emissions.

Agriculture Sector

Crop yield prediction: PCA can be used to identify the key variables that influence crop yield, such as weather conditions, soil characteristics, and irrigation. By analyzing the correlation between variables, PCA can help predict crop yield and optimize crop management practices.
Disease diagnosis: PCA can be used to diagnose plant diseases by analyzing the spectral data of plant leaves. By identifying the principal components that are most affected by disease, PCA can help identify the specific disease that is affecting the plant and facilitate appropriate treatment.
Soil analysis: PCA can be used to analyze soil data and identify the key variables that affect soil quality, such as nutrient levels, pH, and organic matter content. By analyzing the correlation between variables, PCA can help optimize soil management practices and improve crop productivity.
Livestock breeding: PCA can be used to analyze the genetic data of livestock and identify the key variables that influence traits such as growth rate, milk production, and disease resistance. By identifying the principal components that are most important for each trait, PCA can help breeders select animals with desirable traits and improve the productivity of livestock.
Food quality assessment: PCA can be used to assess the quality of agricultural products such as fruits, vegetables, and grains. By analyzing the variance of the data, PCA can help identify the key factors that affect product quality, such as ripeness, texture, and flavor.

Aeronautics and Astronomy

Aircraft Design: PCA can be used to identify the most critical parameters affecting aircraft design, such as weight, performance, and safety, and reduce their dimensionality for optimization.
Flight Data Analysis: PCA can be applied to flight data recordings to identify patterns in aircraft behavior and diagnose problems.
Air Traffic Control: PCA can be used to identify patterns in air traffic and reduce the complexity of the data for efficient analysis.
Galaxy Formation and Evolution: PCA can be used to analyze the spectra of galaxies and identify the principal components that contribute to their formation and evolution.
Exoplanet Detection: PCA can be used to analyze the light curves of stars and identify the principal components that indicate the presence of exoplanets.
Astronomical Imaging: PCA can be used to enhance the quality of astronomical images by reducing noise and removing unwanted features.

LifeSciences

Genomics: PCA can be used to analyze gene expression data and identify the most significant genes that contribute to a specific phenotype. It can also be used to classify samples based on gene expression patterns.
Proteomics: PCA can be used to analyze proteomics data, such as mass spectrometry data, to identify the most significant proteins that contribute to a specific phenotype. It can also be used to classify samples based on protein expression patterns.
Drug Discovery: PCA can be used to analyze the structure-activity relationship (SAR) of a drug and identify the most important structural features that contribute to its activity.
Metabolomics: PCA can be used to analyze metabolomics data and identify the most significant metabolites that contribute to a specific phenotype. It can also be used to classify samples based on metabolite expression patterns.
Neuroscience: PCA can be used to analyze brain imaging data and identify the most significant brain regions that contribute to a specific behavior or disease.

What does magicPCAbring for you ?

“Browse”allows users to upload the dataset and “data ” feature shows the dataset datapoints in an organised tabular view.

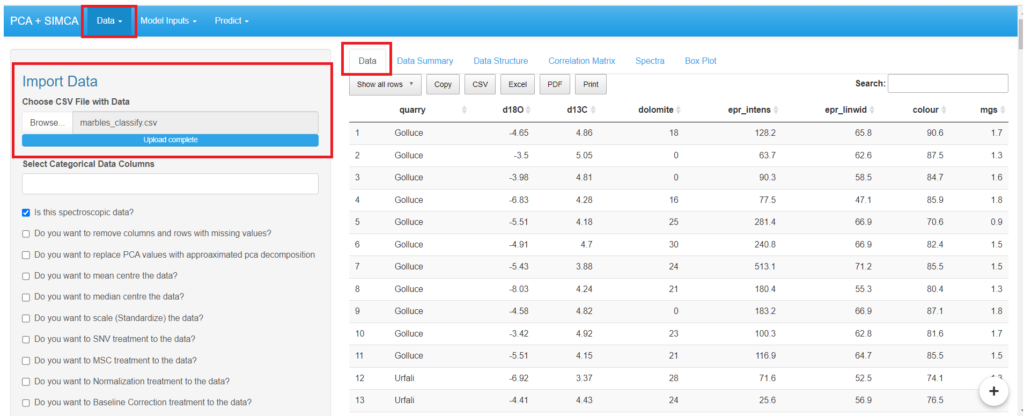
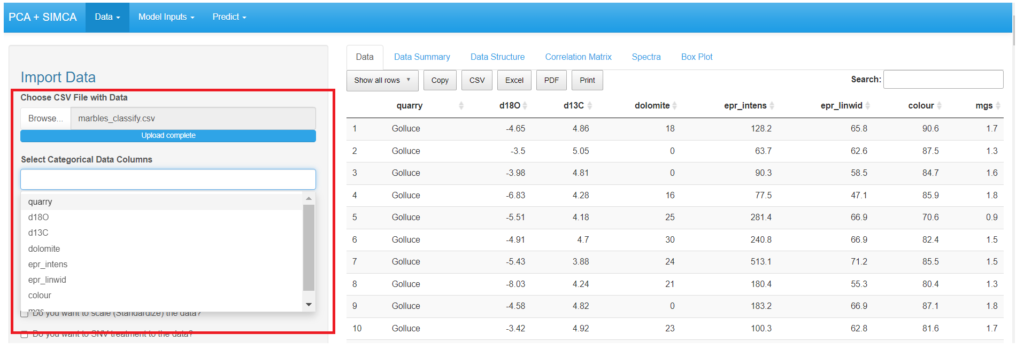
Users must select the “Categorical Data” in the dataset to build the PCA model.

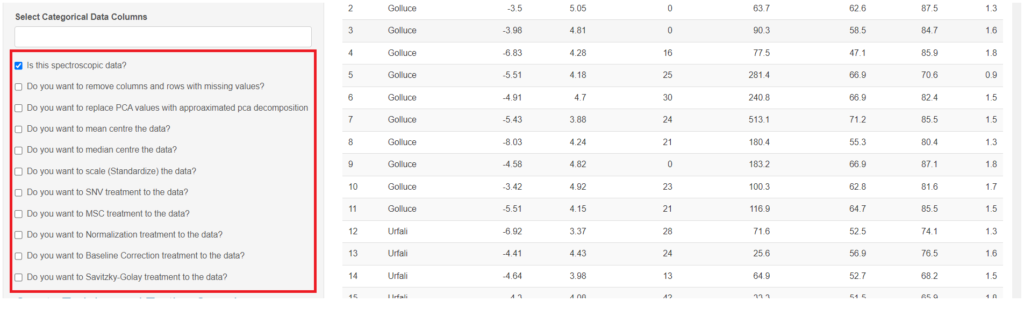
On the left side of the platform , there are multiple checkboxes which will provide users with various features for data points for pre-processing such as “Mean centre”, “median centre”, “standardisation”, “SNV and MSC treatment” , “Normalisation and Baseline Correction”.

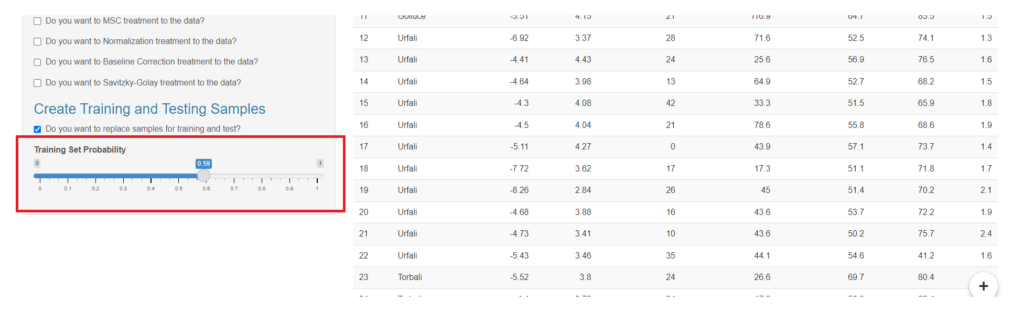
Users can also able to set up the customized ratio of testing and training datasets using “Training set probability”

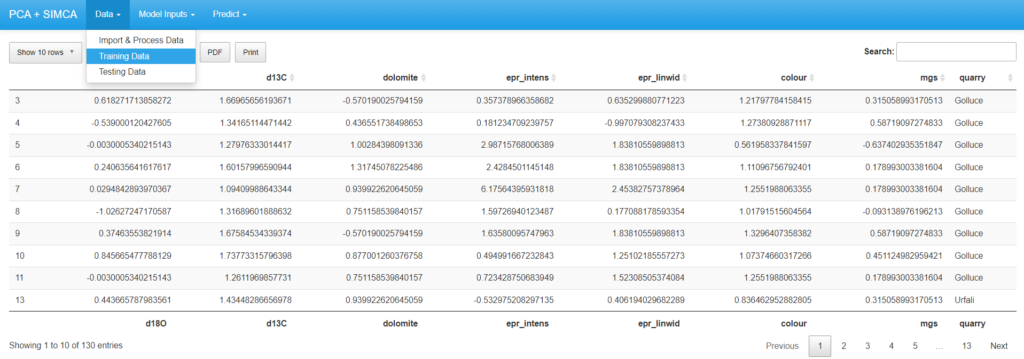
With the help “data ” menu on the top left of the screen, users can select “Training data ” to see the training data points.

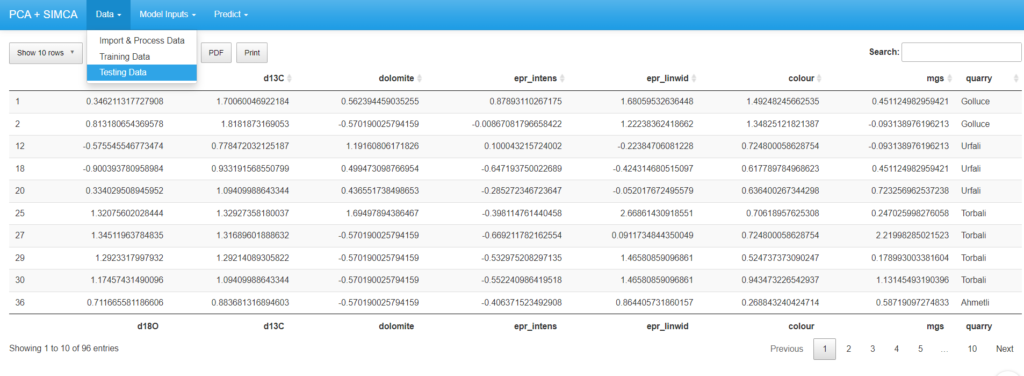
With the help “data ” menu on the top left of the screen, users can select “Testing data ” to see the training data points.

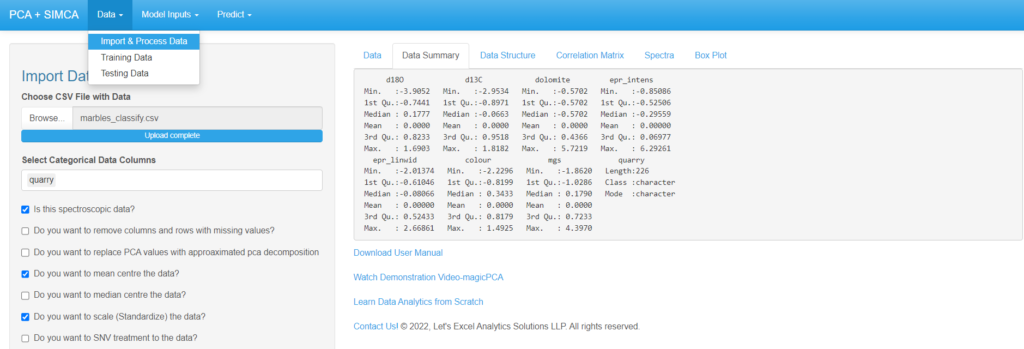
Under the Import & Process Section “Data Summary” allows users to analyze mean, mode, median, and quadrants for each attribute in datasets. It provides calculated values to users with minimal error for better insights.

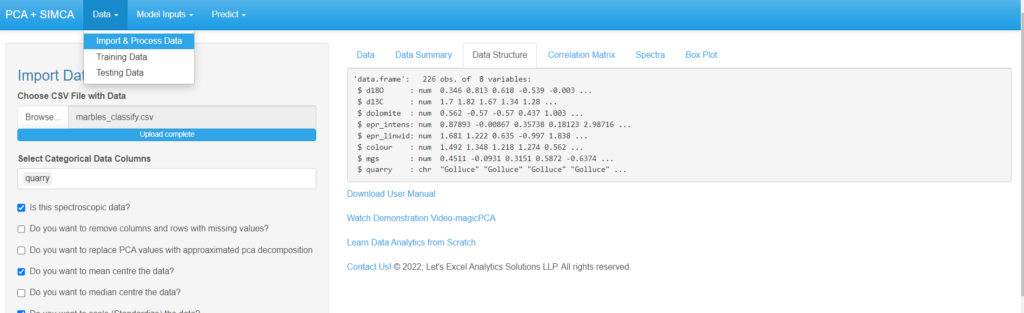
Under the Import & Process Section “Data Structure” allows one to see the data type values of each attribute in the dataset and shows the respective values of each attribute.

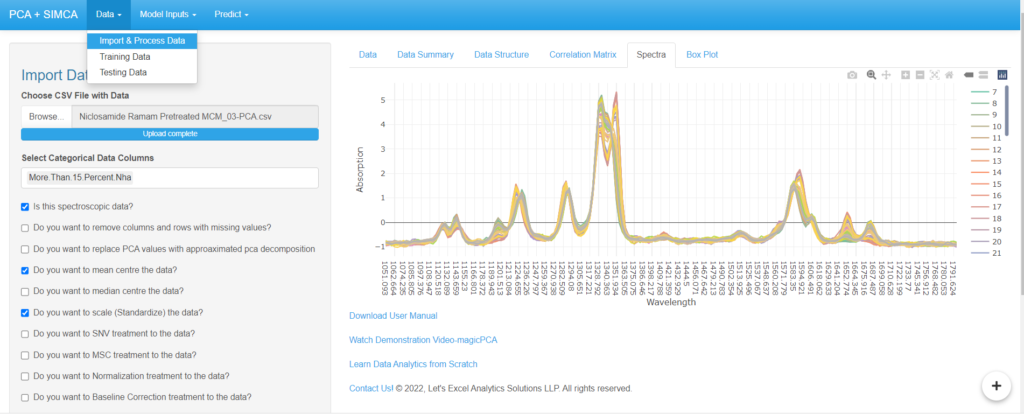
Under the import and process section magicPCA has an option of “Spectra” which shows the spectroscopy view of the dataset.

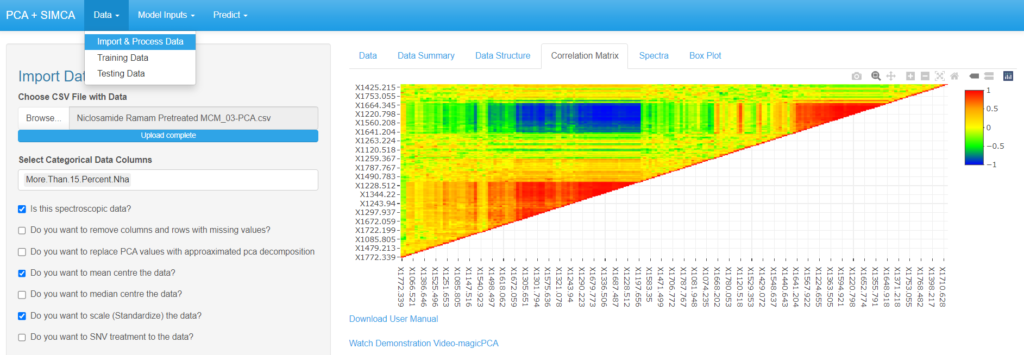
Under the import and process section magicPCA has an option of seeing correlation matrix for exploratory data analysis.

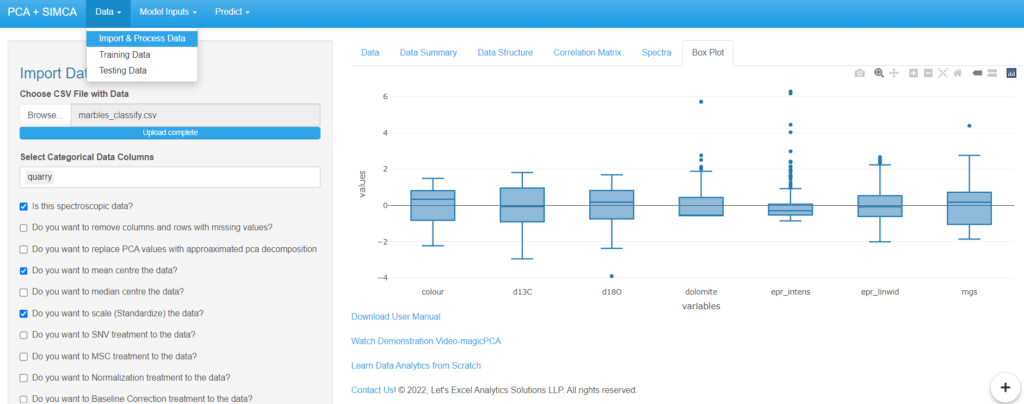
“Box plot” provide user graphical representation of the scores of each principal component. It also provides visualize the distribution of the scores and identify potential outliers in the data.

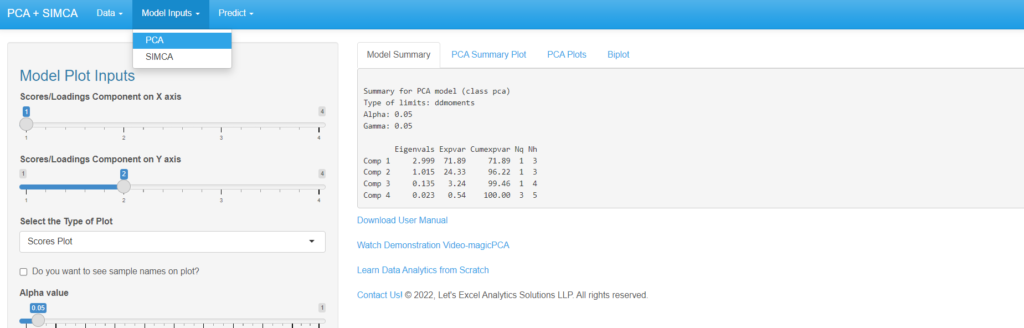
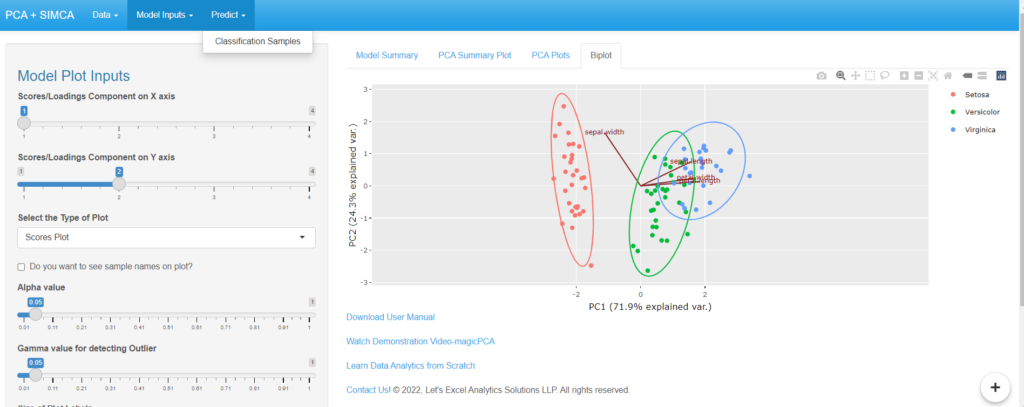
The PCA Model Summary, PCA Summary Plot, PCA Plots, Biplot, and other Model Plots can be seen under “Model Inputs”.

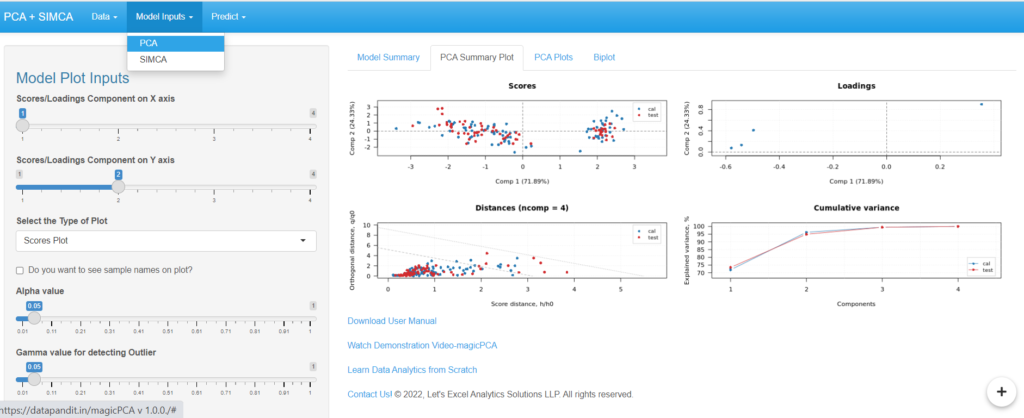
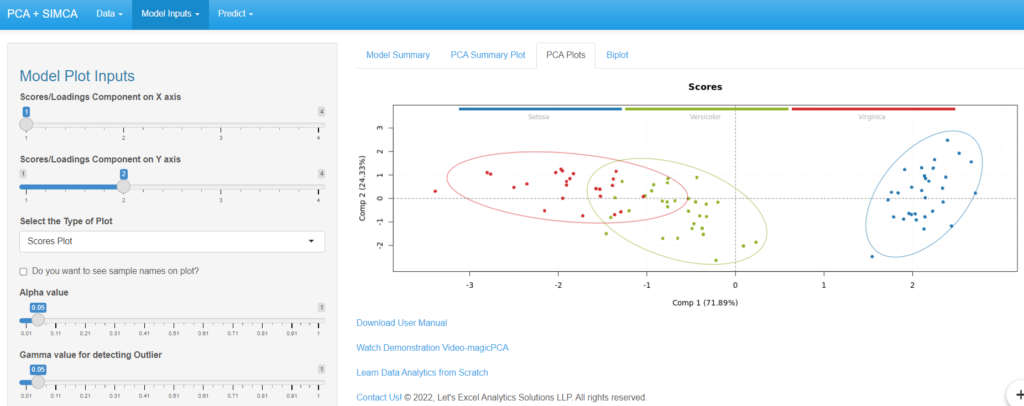
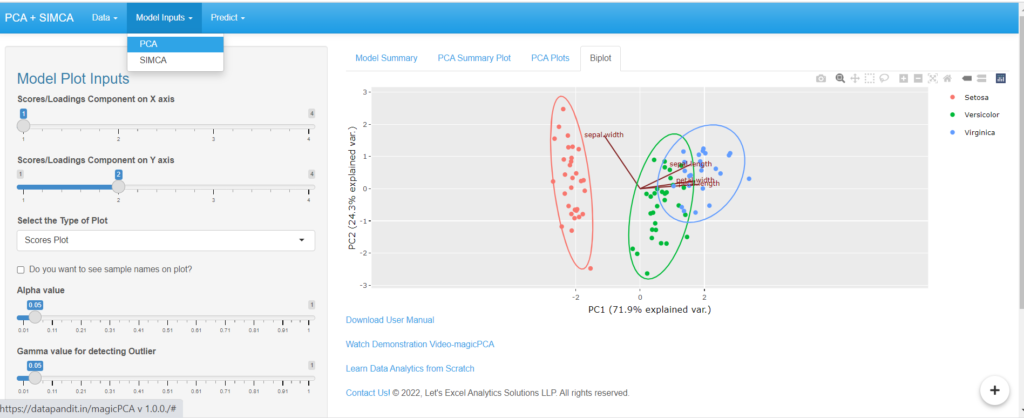
Options to build SIMCA Model are available under the “SIMCA” section in “Model Inputs”.

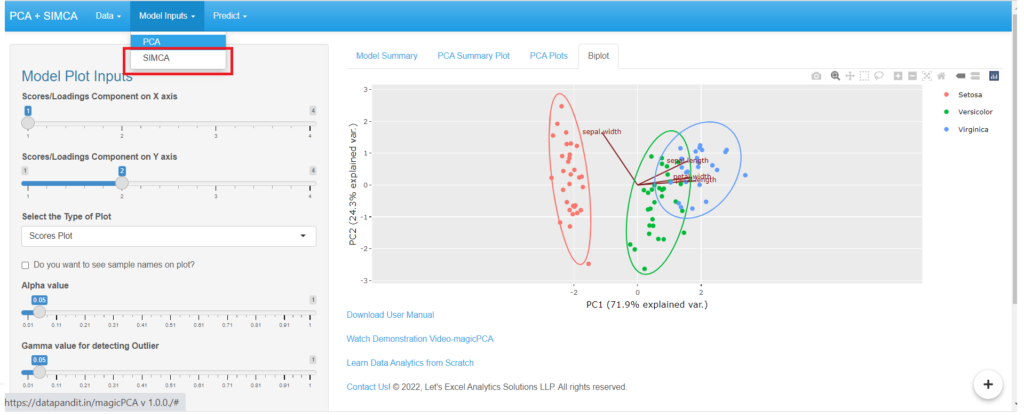
The unknown samples can be predicted using features under the “Predict” Section.

For more detailed guidance on how to use magicPCA to build multivariate models, read this blog article.

Interested in exploring data analytics case studies using magicPCA? Download our free data analytics case studies here Or purchase our Data Analytics Case Studies e-Book on Amazon.